Teorema Limit Bilangan Euler
Limit dalam pelajaran matematika merupakan sebuah konsep dalam bidang ilmu matematik yang biasa dipakai untuk menerangkan suatu sifat dari suatu fungsi.
Barisan bilangan dapat dianggap sebagai fungsi dengan domain bilangan asli. Misalkan diberikan fungsi
dengan bilangan asli.
Rumus fungsi tersebut dapat dikembangkan dengan menerapkan Ekspansi Newton, yaitu
dengan bilangan asli.
Rumus fungsi tersebut dapat dikembangkan dengan menerapkan Ekspansi Newton, yaitu
Untuk , ditulis
Bilangan irasional selanjutnya dikenal sebagai bilangan euler dan dinotasikan dengan huruf . Bilangan ini merupakan konstanta penting dalam bidang kalkulus.
Bilangan irasional selanjutnya dikenal sebagai bilangan euler dan dinotasikan dengan huruf . Bilangan ini merupakan konstanta penting dalam bidang kalkulus.
Kesimpulan:
Modifikasi Limit Euler
Teorema berikut sangat membantu dalam menyelesaikan persoalan mengenai penentuan nilai limit euler.
Teorema 1. Apabila  dan
dan  maka
maka
contoh 1 :
Tentukan  .
.
Penyelesaian.
Penyelesaian.
Apabila berturut-turut diambil  dan
dan  maka
maka
Berdasarkan teorema di atas diperoleh
Contoh 2 :
Tentukan  .
.
Penyelesaian.
Penyelesaian.
Apabila diambil  dan
dan  maka
maka
Berdasarkan teorema di atas diperoleh
Limit Fungsi Trigonometri
nilai terdekat pada suatu sudut fungsi trigonometri. Perhitungan limit fungsi ini bisa langsung disubtitusikan seperti misalnya namun ada fungsi trigonometri yang harus diubah dahulu ke identitas trigonometri untuk limit tak tentu yaitu limit yang apabila langsung subtitusikan nilainya bernilai 0, bisa juga untuk limit tak tentu tidak harus memakai identitas tetapi menggunakan teorema limit trigonometri atau ada juga yang memakai identitas dan teorema. Maka apabila suatu fungsi limit trigonometri di subtitusikan nilai yang mendekatinya menghasilkan dan maka harus menyelesaikan dengan cara lain.
Macam – Macam Trigonometri
Limit Fungsi Trigonometri untuk x Mendekati Suatu Bilangan
Cara menentukan nilai limit fungsi trigonometri untuk x mendekati suatu bilangan c dapat secara mudah diperoleh dengan melakukan substitusi nilai c pada fungsi trigonometrinya. Persamaan rumus limit fungsi trigonometri diberikan seperti pada gambar di bawah.

Berikut ini adalah contoh soal penggunaan rumus limit fungsi trigonometri untuk x mendekati suatu bilangan.
ada kasus tertentu, nilai limit untuk x mendekati bilangan 0 akan menghasilkan  . Misalnya pada kasus berikut.
. Misalnya pada kasus berikut.
Jika dilakukan substitusi secara langsung, nilai limitnya adalah
Limit Fungsi Trigonometri untuk x Mendekati 0 (Nol)
Dalam pembahasan limit fungsi trigonometri, terdapat berbagai rumus yang dapat disebut sebagai “properti” untuk menyelesaikan soal limit fungsi trigonometri. Kumpulan properti tersebut dapat dilihat pada daftar rumus limit trigonometri yang diberikan di bawah.

Teorema Limit Trigonometri
1. Teorema A
2. Teorema B
1. Tentukan nilai limit fungsi trigonometri dibawah!
Pembahasan:
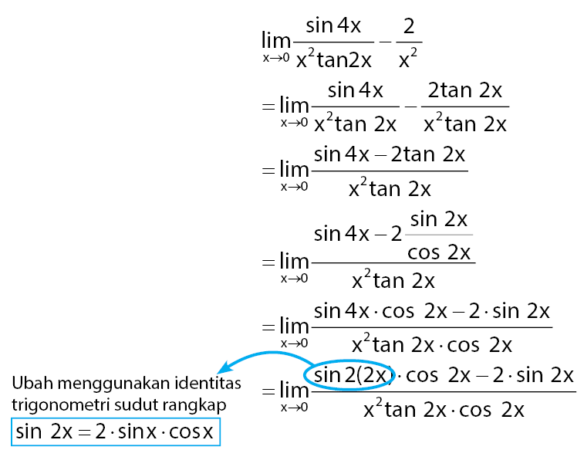
Dengan melakukan transformasi menggunakan identitas trigonometri rumus fungsi sinus sudut rangkap akan diperoleh persamaan di bawah.
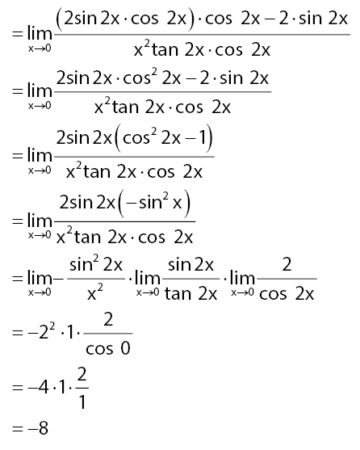
Referensi : https://www.youtube.com/watch?v=9_KHAaZ_TUk


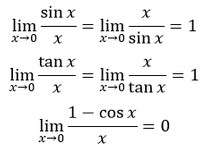
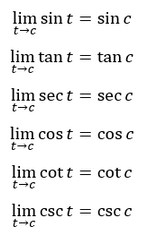
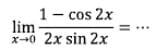

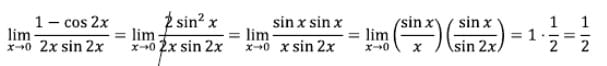
Komentar
Posting Komentar